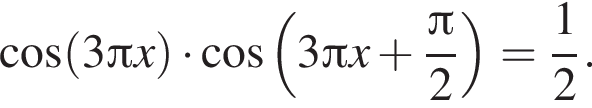Результат упрощения выражения 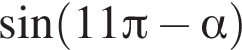 равен:
равен:


Результат упрощения выражения 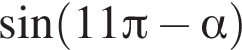 равен:
равен:


Упростите выражение 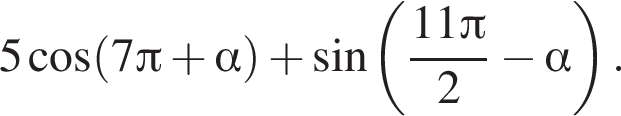
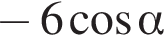
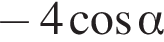

Выберите три верных утверждения:
1) если 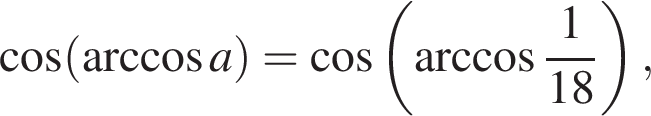 то
то 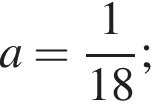
2) если 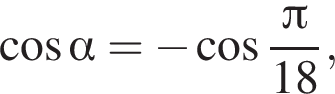 то
то 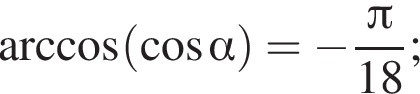
3) если 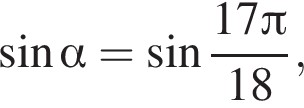 то
то 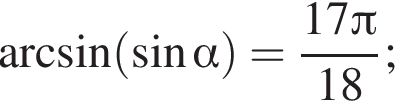
4) если 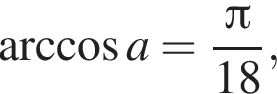 то
то 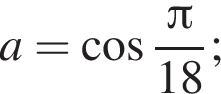
5) если 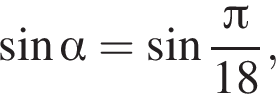 то
то 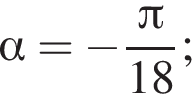
6) если 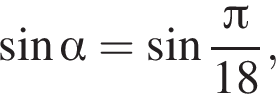 то
то 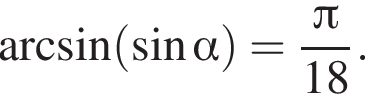
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 123.
Упростите выражение 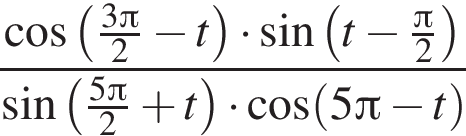
Найдите (в градусах) наименьший корень уравнения 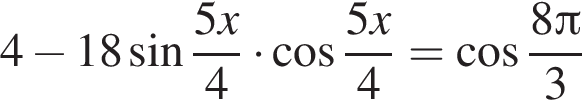 на промежутке (−180°; 0°).
на промежутке (−180°; 0°).
Найдите сумму (в градусах) наименьшего положительного и наибольшего отрицательного корней уравнения 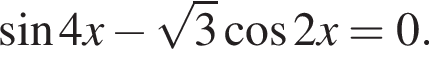
Найдите (в градусах) наибольший корень уравнения
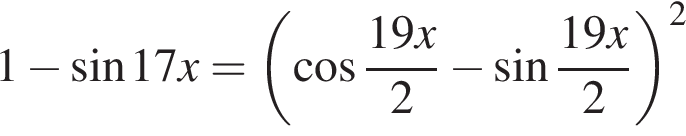
Найдите произведение наименьшего корня (в градусах) на количество различных корней уравнения  на промежутке (−90°; 90°).
на промежутке (−90°; 90°).
Найдите (в градусах) корень уравнения  на промежутке (0°; 45°).
на промежутке (0°; 45°).
Найдите наименьший положительный корень уравнения 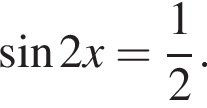
Найдите наименьший положительный корень уравнения 

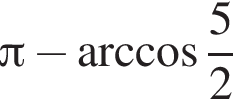
Найдите (в градусах) наименьший корень уравнения 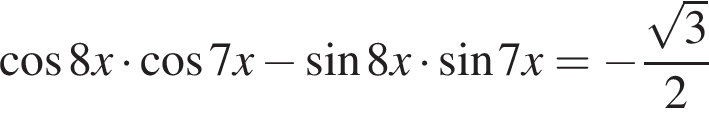 на промежутке
на промежутке 
Найдите (в градусах) сумму корней уравнения 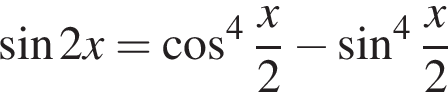 на промежутке [−223°; 333°].
на промежутке [−223°; 333°].
Найдите (в градусах) сумму различных корней уравнения 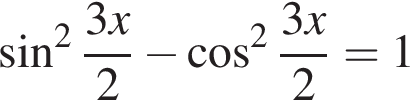 на промежутке
на промежутке 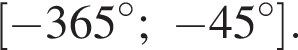
Найдите сумму корней уравнения 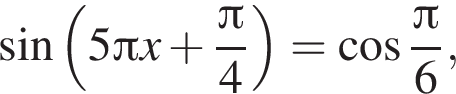 принадлежащих промежутку
принадлежащих промежутку 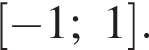
Найдите (в градусах) наибольший отрицательный корень уравнения 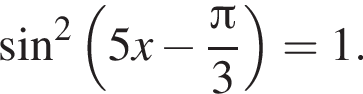
Найдите количество корней уравнения 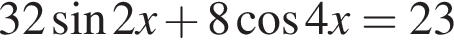 на промежутке
на промежутке 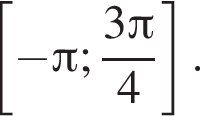
Решите уравнение 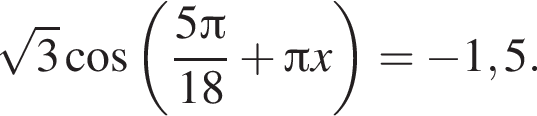 В ответ запишите увеличенное в 3 раза произведение наибольшего корня (в радианах) на количество корней этого уравнения на промежутке [3; 9].
В ответ запишите увеличенное в 3 раза произведение наибольшего корня (в радианах) на количество корней этого уравнения на промежутке [3; 9].
Найдите (в градусах) сумму корней уравнения  на промежутке (110°; 170°).
на промежутке (110°; 170°).
Найдите (в градусах) сумму различных корней уравнения 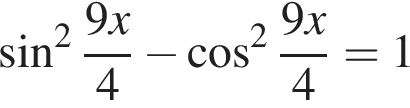 на промежутке [−235°; −35°].
на промежутке [−235°; −35°].
Найдите (в градусах) наименьший корень уравнения 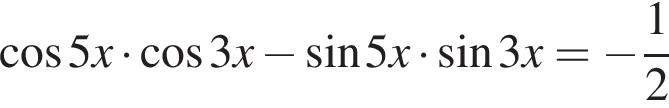 на промежутке (−80°; 0°).
на промежутке (−80°; 0°).
Укажите (в градусах) наименьший положительный корень уравнения 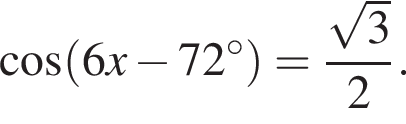
Вычислите сумму наибольшего отрицательного и наименьшего положительного корней уравнения